For months, Taleb has been arguing that the correlation between wealth and IQ is non-existent. He posted the following scatter plot from the Zagorsky, 2007 study below, but note how he chops off the bottom:
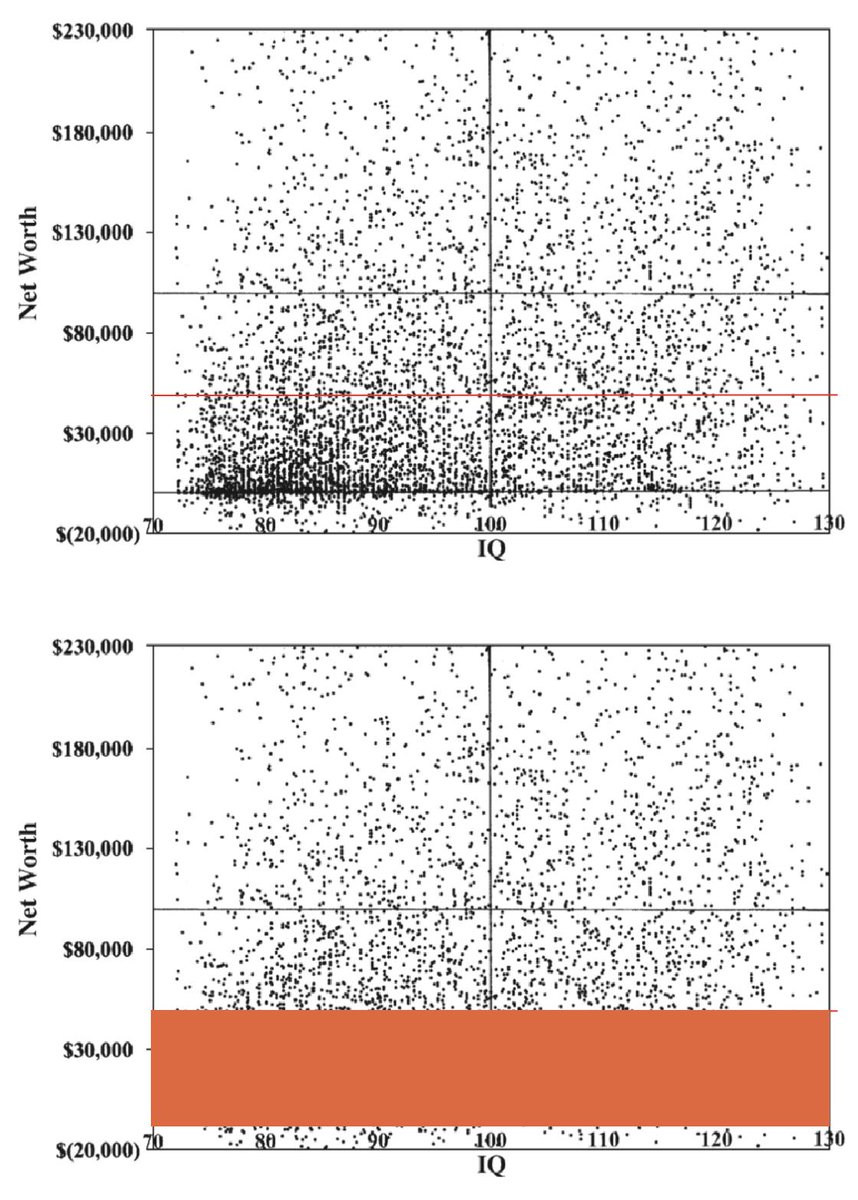
It’s worse than I thought because in my original post I did not mention the fact that Taleb blocked out the data. This is important because the the barchart plot measures median wealth for each IQ level, so by chopping off the bottom, the mean matters more, so therefore the correlation weakens and may be non-existent. This is because there is a dense clustering of people with IQs between 70 and 100 who have a low net worth. Also, the top is chopped off at $230k, because the y-axis of the plot does not go beyond that, which also bolsters Taleb’s thesis. You cannot do that though. Truncating/omitting the data that disproves your thesis epitomizes intellectual dishonesty.
A Google search shows that Taleb is not the only one who holds this wrong belief that IQ is not predictive of net worth. I have seen the Zagorsky study referenced even as recently as 2015 to support this erroneous conclusion.
There are three flaws with the Zagorsky study:
1. The top is truncated at $230k. It’s conceivable that very-high net worth (>$1mm) is strongly positively correlated with IQ.
2. It uses old data. The study follows “young baby boomers 21 times between 1979 and 2004,” which is many decades ago. However, recent trends in technology, ‘the information age’, automation, and the post-2009 bull market has created an economic environment that likely strengthens the correlation between wealth and IQ, whereas in the 50’s-90’s, the correlation was weaker.
3. Today’s investors have many more options to invest and grow their wealth, compared to generations ago, such as low-cost index funds, 401ks, roth IRAs, etc.
I think “Reddit test” is better, because it’s most applicable to today’s economic environment and how people define actual wealth. Instead of finding correlations between all levels of wealth, let’s just focus on wealth above $500,000, which is considered the minimum threshold for a “high net-worth investor,” because that is what people have in mind when they think of ‘wealth’, not the difference between $30k versus $100k. Although this cut-off may seem arbitrary, we’re interested in uncommonly high wealth; the cut-off could just as easily be $400,000 or $600,000, but if it’s too high then finding enough data will be difficult. And let’s restrict age to <40, because older people tend to be wealthier than young people, by virtue of working longer and compounding money longer. We're interested in studying people who accumulate a lot of wealth early in life. It's more impressive when a young person accumulates a high-net-worth than an older person who does so. It is also possible to run this on other IQ intervals, such as 110-120, and 100-110, etc. to test for robustness of findings. The odds ratio is a useful tool for quantifying the strength of the association between two variables, those being high-net-worth and IQ. So based on the above conditions, according to empirical evidence of self-reported net worth on personal finance and investing subs by Reddit users, my hypothesis is, the odds ratio of having an IQ above 120 and a net worth >$500,000 is way higher than a control average-IQ group. I predict it’s not even close. Maybe you’ll get a single tradesman who worked 80 hours a week or a lucky entrepreneur or two in a low-tech field, but it’s high-IQ all the way. This blows out of the water the argument that there is no link between the attainment of a high-net-worth at an early age and IQ. People like Taleb think their out-dated, manipulated scatter plots can override the manifestly obvious empirical evidence that proves them wrong.
So the experiment could work as follows: suppose, hypothetically, you have a sample of 100 people with IQs below 120, and 30 with IQs above 120. And in the first group, 4 have a reported net-worth of over $500,000, and in the second group it’s 6.
So using an odds ratio calculator (with the variables a=30,c=100,b=6,d=4) to expedite the computation, we have:
Odds ratio 0.2000
95 % CI: 0.0529 to 0.7557
z statistic 2.373
Significance level P = 0.0176
Which is a low enough p-value to be considered statistically significant, with a confidence level of over 98%.
To test the robustness of this, one can modify the parameters, such as lowering or raising IQ and the net-worth threshold.