After a brief attempt at a reprieve yesterday, the death spiral resumes:
That is why I don’t sweat it, cuz gains never hold in the world of crypto, in which whoever loses the least amount of money is the biggest winner. If you broke even on your crypto investment, consider yourself among the lucky few.
He’s right…it’s crap:
btc is crap
— Moonbag (@Cheellox) August 24, 2023
Where is the bottom? Way lower.
Meanwhile, tech stocks keep going up and up (as crypto crashes and as predicted would happen), staging huge recovery thanks to massive Nvidia earnings last night. Nvidia stock crossed $500 this morning, whereas BTC can’t even hold $27k. Pathetic indeed.
The future is not crypto, but instead big tech companies. Instead of the decentralized ‘network state’, it’s more like the centralized tech ‘surveillance state’. Balaji and other people got this wrong by assuming it would be crypto. Of course the federal government is going to support big tech and oppose crypto. When the govt. made all those Jan 6th arrests, where did they get the info? From GPS and social media accounts.
All $ flowing into a handful of large cap tech stocks, like Meta and Nvidia, and out of everything else (except for retail like Walmart, McDonald’s). Everything else is weak. Unless you own one of these dozen or so large companies, my position has always been there is no reason to own individual stocks. Too much risk relative to reward. Just stick with QQQ or index funds.
Having already mastered finance, econ, trading etc. I am setting my sights on the next new thing, which has a higher ‘IQ ceiling’ than those aforementioned items, that being math. Investing is considered hard, but it’s pretty obvious what the best strategies are. It’s not like you need advanced degrees figure this stuff out. Same for predicting the economy: GDP and stocks tend to go up over the long term.
One of things I investigated years ago is integrals of the form:
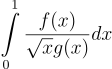 in which f(x) and g(x) are polynomials
in which f(x) and g(x) are polynomials
The astute reader can see it yields an inverse trig function via partial fraction decomposition . But the question is what values of polynomials yield ‘nice’, fast-converging series. By nice I mean which does not involve radicals or ‘root objects’–preferably, only integers. Obviously it’s possible to derive series by just inverting g(x)=0 but the result is likely messy and inelegant. [Indeed it is possible for root objects to yield integers even if individually they are irrational, notably when finding the nth Fibonacci number.] This is an area of some active research in math involving integrals like above. Inspired by an earlier paper I found one such integral that yields a series that even years later and subsequent papers published, has not been surpassed, even with the aid of algebraic math software that can perform symbolic manipulation to try to find such expressions for various polynomial choices. Some papers come close but not quite there. I am still surprised it exists, because it’s such an outlier.
